11.1 z-Test for Comparing Proportions

Gordon E. Sarty

11. Comparing Proportions

11.1 z-Test for Comparing Proportions

In Section 9.4 we covered a one-sample test for proportions using the $z$ approximation to the binomial distribution. Here we want to compare a proportion $p_{1}$ in one population with $p_{2}$ in another population, a two-sample test for proportions, also using the $z$ approximation to the binomial distribution. Define

$\hat{p}_{1} = \frac{x_{1}}{n_{1}} \mbox{\ \ \ \ and\ \ \ \ } \hat{p}_{2} = \frac{x_{2}}{n_{2}}$

where $x_{1}$ and $x_{2}$ are the number of items of interest in the samples from the two populations and $n_{1}$ and $n_{2}$ are their sample sizes. Also define the corresponding $q_{1} = 1 - p_{1}$ , $q_{2} = 1 - p_{2}$ , $\hat{q}_{1} = 1 - \hat{p}_{1}$ and $\hat{q}_{2} = 1 -\hat{ }p_{2}$ . The hypotheses we want to test is

$H_{0}: p_{1} = p_{2} \hspace*{3em} H_{1}: p_{1} \neq p_{2}$

which is equivalent to

$H_{0}: p_{1} - p_{2} = 0 \hspace*{3em} H_{1}: p_{1} - p_{2} \neq 0$

If $n_{1}p_{1}, n_{1}q_{1}, n_{2}p_{2}$ , and $n_{2}q_{2}$ are all $> 5$ then the appropriate normal distribution will provide a good approximation to the relevant binomial distribution and we can use the following test statistic to test the hypotheses

$z_{\rm test} = \frac{\hat{p}_{1} - \hat{p}_{2}}{\sqrt{\bar{p}\bar{q} \left( \frac{1}{n_{1}} + \frac{1}{n_{2}} \right)}}$

where

$\bar{p} = \frac{x_{1}+x_{2}}{n_{1}+n_{2}} \hspace*{3em} \bar{q} = 1 -\bar{p}$

are the proportions of items of interest and not of interest in the two samples combined.

Example 11.1 : In a nursing home study we are interested in the proportions of nursing homes that have vaccination rates of less than 80 $\%$ . The two populations we want to compare are small nursing homes and large nursing homes. In a sample of 34 small nursing homes, 12 were found to have a vaccination rate of less than 80 $\%$ . In a sample of 24 large nursing homes, 17 were found to have a vaccination rate of less than 80 $\%$ . At $\alpha = 0.05$ is there a difference in the proportions of small and large nursing homes with vaccination rates of less than 80 $\%$ ?

Solution :

0. Data reduction.

First define: population 1 = small nursing homes and population 2 = large nursing homes. Then compute the proportions:

$\hat{p}_{1} = \frac{x_{1}}{n_{1}} = \frac{12}{34} = 0.35 \hspace{4em} \hat{p}_{2} = \frac{x_{2}}{n_{2}} = \frac{17}{24} = 0.71$

$\bar{p} = \frac{x_{1} + x_{2}}{n_{1} + n_{2}} = \frac{12+17}{34+24} = \frac{29}{58} = 0.5 \hspace{4em} \bar{q} = 1 - \bar{p} = 1 - 0.5 = 0.5$

1. Hypotheses.

$H_{0}: p_{1} = p_{2} \hspace*{3em} H_{1}: p_{1} \neq p_{2}$

2. Critical statistic.

Use Table F, the last ( $z$ ) line in the column for a two-tailed test at $\alpha = 0.05$ : $z_{\rm crit} = \pm 1.96$

3. Test statistic.

$\begin{eqnarray*} z_{\rm test} & = & \frac{\hat{p}_{1} - \hat{p}_{2}}{\sqrt{\bar{p}\bar{q} \left( \frac{1}{n_{1}} + \frac{1}{n_{2}} \right)}} \\ z_{\rm test} & = & \frac{0.35 - 0.71}{\sqrt{(0.5)(0.5) \left( \frac{1}{34} + \frac{1}{24} \right)}} \\ z_{\rm test} & = & \frac{-0.36}{0.1333} \\ z_{\rm test} & = & -2.7 \end{eqnarray*}$

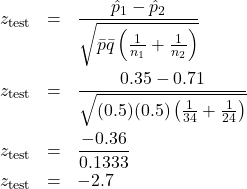
4. Decision.

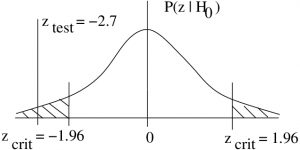
Reject $H_{0}$ .

5. Interpretation.

There is enough evidence, from a $z$ proportions test at $\alpha = 0.05$ to support the observation that large nursing homes have worse vaccination rates than small nursing homes. Make sure your parents end up in a small nursing home. (Note that rejection of $H_{0}$ in a one-tail test allows us to believe the direction of difference given by the sample data.)

▢

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Share This Book