14. Correlation and Regression
14.2 Correlation
The correlation coefficient we will use here is called the “Pearson product moment correlation coefficient” and will be represented by the following symbols :
![]() — population correlation
— population correlation
![]() — sample correlation
— sample correlation
The correlation is always a number between ![]() and
and ![]() :
: ![]() and
and ![]() . If
. If ![]() (or
(or ![]() ) equals 0 then that means there is no correlation between
) equals 0 then that means there is no correlation between ![]() and
and ![]() . A minus sign means a minus slope, a plus sign means a positive slope.
. A minus sign means a minus slope, a plus sign means a positive slope.
The formula for ![]() is[1] :
is[1] :
(14.1) ![]()
Example 14.1 : Compute the correlation between ![]() and
and ![]() for the data on Section 14.1 used for the scatter plot.
for the data on Section 14.1 used for the scatter plot.
Solution : To compute ![]() , first make a table, fill in the data columns (on the right of the double vertical line below), fill in the other computed columns, sum the columns and finally plug the sums into the formula for
, first make a table, fill in the data columns (on the right of the double vertical line below), fill in the other computed columns, sum the columns and finally plug the sums into the formula for ![]() :
:
| Subject | |||||
|---|---|---|---|---|---|
| A | 6 | 82 | 492 | 36 | 6724 |
| B | 2 | 86 | 172 | 4 | 7396 |
| C | 15 | 43 | 645 | 225 | 1849 |
| D | 9 | 74 | 666 | 81 | 5476 |
| E | 12 | 58 | 696 | 144 | 3364 |
| F | 5 | 90 | 450 | 25 | 8100 |
| G | 8 | 78 | 624 | 64 | 6084 |
Plug in the numbers :
![Rendered by QuickLaTeX.com \begin{eqnarray*} r & = & \frac{n(\sum xy) - (\sum x)(\sum y)}{\sqrt{[n (\sum x^{2}) - (\sum x)^{2}][n (\sum y^{2}) - (\sum y)^{2}]}}\\ & = & \frac{7(3745) - (57)(511)}{\sqrt{[7 (579) - (57)^{2}][7 (38993) - (511)^{2}]}}\\ & = & -0.944 \end{eqnarray*}](https://www.saskoer.ca/app/uploads/quicklatex/quicklatex.com-8c33bdfa75c01f4c580b61d150c875f8_l3.png)
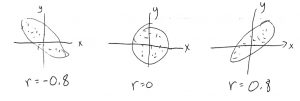
Here there is a strong negative relationship between ![]() and
and ![]() . That is, as
. That is, as ![]() goes up,
goes up, ![]() goes down with a fair degree of certainty. Note the
goes down with a fair degree of certainty. Note the ![]() is not the slope. All we know here, from the correlation coefficient, is that the slope is negative and the scatterplot ellipse is long and skinny.
is not the slope. All we know here, from the correlation coefficient, is that the slope is negative and the scatterplot ellipse is long and skinny.
▢
Standard warning about correlation and causation : If you find that ![]() and
and ![]() are highly correlated (i.e.
are highly correlated (i.e. ![]() is close to
is close to ![]() or
or ![]() ) then you cannot say that
) then you cannot say that ![]() causes
causes ![]() or that
or that ![]() causes
causes ![]() or that there is and causal relationship between
or that there is and causal relationship between ![]() and
and ![]() at all. In other words, it is true that if
at all. In other words, it is true that if ![]() causes
causes ![]() or that
or that ![]() causes
causes ![]() then
then ![]() will be correlated with
will be correlated with ![]() but the reverse implication does not logically follow. So beware of looking for relations between variables by looking at correlation alone. Simply finding correlations by themselves doesn’t prove anything.
but the reverse implication does not logically follow. So beware of looking for relations between variables by looking at correlation alone. Simply finding correlations by themselves doesn’t prove anything.
The significance of ![]() is assessed by a hypothesis test of
is assessed by a hypothesis test of
![]()
To test this hypothesis, you need to convert ![]() to
to ![]() via:
via:
![]()
and use ![]() to find
to find ![]() . The Pearson Correlation Coefficient Critical Values Table offers a shortcut and lists critical
. The Pearson Correlation Coefficient Critical Values Table offers a shortcut and lists critical ![]() values that correspond to the critical
values that correspond to the critical ![]() values.
values.
Example 14.2 : Given ![]() ,
, ![]() and
and ![]() , test if
, test if ![]() is significant.
is significant.
Solution :
1. Hypothesis. ![]()
2. Critical statistic.
From the t Distribution Table with ![]() and
and ![]() for a two-tailed test find
for a two-tailed test find
![]()
As a short cut, you can also look in the Pearson Correlation Coefficient Critical Values Table for ![]() ,
, ![]() to find the corresponding
to find the corresponding
![]()
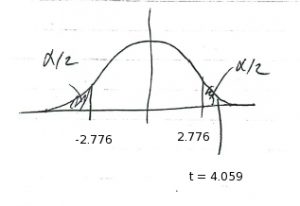
3. Test statistic.
![Rendered by QuickLaTeX.com \[ t_{\mbox{test}} = r \sqrt{\frac{n-2}{1 - r^{2}}} = 0.897 \sqrt{\frac{6-2}{1 - (0.897)^{2}}} = 4.059 \]](https://www.saskoer.ca/app/uploads/quicklatex/quicklatex.com-e02446450370504b7c47e43d6cabdb78_l3.png)
4. Decision.
Using the ![]() :
:
or using the Pearson Correlation Coefficient Critical Values Table short cut :
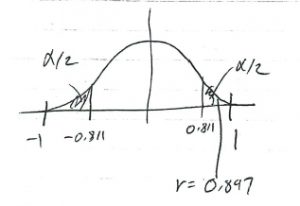
we conclude that we can reject ![]() .
.
5. Interpretation. The correlation is statistically significant at ![]() .
.
▢
- The formula for
 is the same with all
is the same with all 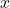 and
and 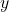 in the population used. ↵
in the population used. ↵

