"

14. Correlation and Regression

14.5 Linear Regression

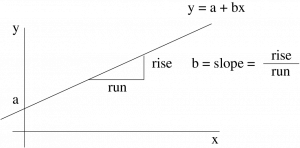
Linear regression gives us the best equation of a line through the scatter plot data in terms of least squares. Let’s begin with the equation of a line:

    \[ y = a + bx \]

where a is the intercept and b is the slope.

The data, the collection of (x,y) points, rarely lie on a perfect straight line in a scatter plot. So we write

    \[ y^{\prime} = a + b x \]

as the equation of the best fit line. The quantity y^{\prime} is the predicted value of y (predicted from the value of x) and y is the measured value of y. Now consider :

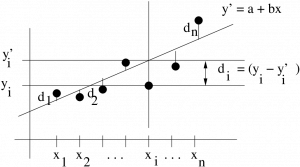
The difference between the measured and predicted value at data point i, d_{i} = y_{i} - y^{\prime}_{i}, is the deviation. The quantity

    \[ d^{2}_{i} = (y_{i} - y^{\prime}_{i})^{2} = (y_{i} - (a + b x_{i}))^{2} \]

is the squared deviation. The sum of the squared deviations is

    \[ E = \sum_{i=1}^{n} d_{i}^{2} = \sum_{i=1}^{n} (y_{i} - (a + b x_{i}))^{2} \]

The least squares solution for a and b is the solution that minimizes E, the sum of squares, over all possible selections of a and b. Minimization problems are easily handled with differential calculus by solving the differential equations:

    \[ \frac{\partial E}{\partial a}=0 \;\;\;\;\; \mbox{and} \;\;\;\;\; \frac{\partial E}{\partial b}=0 \]

The solution to those two differential equations is

    \[ a = \frac{(\sum y_{i})(\sum x_{i}^{2}) - (\sum x_{i})(\sum x_{i} y_{i})}{n(\sum x_{i}^{2}) - (\sum x_{i})^{2}} \]

and

    \[ b = \frac{n(\sum x_{i} y_{i}) - (\sum x_{i})(\sum y_{i})}{n(\sum x_{i}^{2}) - (\sum x_{i})^{2}} \]

Example 14.3 : Continue with the data from Example 14.1 and find the best fit line. The data again are:

Subject x y xy x^{2} y^{2}
A 6 82 492 36 6724
B 2 86 172 4 7396
C 15 43 645 225 1849
D 9 74 666 81 5476
E 12 58 696 144 3364
F 5 90 450 25 8100
G 8 78 624 64 6084
n=7 \sum x=57 \sum y=511 \sum xy=3745 \sum x^{2}=579 \sum y^{2}=38993

Using the sums of the columns, compute:

    \begin{eqnarray*} a & = & \frac{(\sum y_{i})(\sum x_{i}^{2}) - (\sum x_{i})(\sum x_{i} y_{i})}{n(\sum x_{i}^{2}) - (\sum x_{i})^{2}} \\ & = & \frac{(511)(579) - (57)(3745)}{(7)(579) - (57)^{2}} \\ & = & 102.493 \end{eqnarray*}

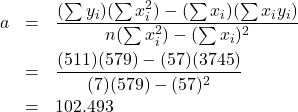
and

    \begin{eqnarray*} b & = & \frac{n(\sum x_{i} y_{i}) - (\sum x_{i})(\sum y_{i})}{n(\sum x_{i}^{2}) - (\sum x_{i})^{2}} \\ & = & \frac{(7)(3745) - (57)(511)}{(7)(579) - (57)^{2}} \\ & = & -3.622 \end{eqnarray*}

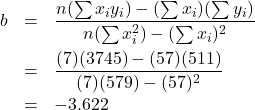
So

    \begin{eqnarray*} y^{\prime} & = & a + bx \\ y^{\prime} & = & 102.493 - 3.622 x \end{eqnarray*}

▢

14.5.1: Relationship between correlation and slope

The relationship is

    \[ r = \frac{b s_{x}}{s_{y}} \]

where

    \begin{eqnarray*} s_{x} & = & \sqrt{\frac{\sum_{i=1}^{n}(x_{i} - \overline{x})^{2}}{n-1}} \\ s_{y} & = & \sqrt{\frac{\sum_{i=1}^{n}(y_{i} - \overline{y})^{2}}{n-1}} \end{eqnarray*}

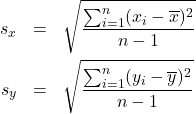
are the standard deviations of the x and y datasets considered separately.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book