14.7 Confidence Interval for y′ at a Given x

Gordon E. Sarty

14. Correlation and Regression

14.7 Confidence Interval for y′ at a Given x

At a fixed $x$ (that is important to remember) the confidence interval for $y$ is

$y^{\prime} - E < y < y^{\prime} + E$

where

$E = t_{\cal{C}} \; s_{\mbox{est}} \sqrt{1+ \frac{1}{n} + \frac{n(x - \overline{x})^{2}}{n(\sum x^{2})-(\sum x)^{2}}}$

where, as usual, $t_{\cal{C}}$ comes from the t Distribution Table with $\nu = n-2$ .

Example 14.5 : Continuing from Example 14.4 (so you can see how an exam will go), say we want to predict the grade ( $y$ ) in terms of a 95 $\%$ confidence interval for the number of absences ( $x$ ) equal to 10.

First, find the value predicted from the regression line, which we previously found to be :

$y^{\prime} = 102.493 - 3.622 x$

at $x = 10$ . The result is

$y^{\prime} = 102.493 - 3.622 (10) = 66.273$

Furthermore, from the last example, we found

$s_{\mbox{est}} = 6.06$

and, from the completed data table (Example 14.3)

$\sum x = 57 \;\;\; \sum x^{2} = 579$

We still need $t{\cal{C}}$ and $\overline{x}$ . Using our sums:

$\overline{x} = \frac{\sum x}{n} = \frac{57}{7} = 8.143$

and from t Distribution Table for the 95 $\%$ confidence interval, $\nu = 7-2 = 5$ we get

$t{\cal{C}} = 2.571$

Now we compute $E$ :

$\begin{eqnarray*} E & = & t_{\cal{C}} \; s_{\mbox{est}} \sqrt{1+ \frac{1}{n} + \frac{n(x - \overline{x})^{2}}{n(\sum x^{2})-(\sum x)^{2}}}\\ E & = & (2.571) \; (6.06) \sqrt{1+ \frac{1}{7} + \frac{7(10 - 8.143)^{2}}{7(579)-(52)^{2}}}\\ E & = & 15.58026 \sqrt{1 + 0.1428571 + \frac{24.139}{804}}\\ E & = & 16.77 \end{eqnarray*}$

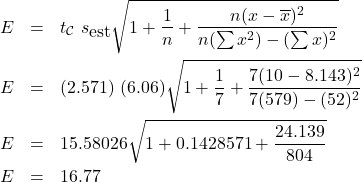
So

$\begin{eqnarray*} y^{\prime} - E & < y < & y^{\prime} + E \\ 66.273 - 16.77 & < y < & 66.273 + 16.77 \\ 49.5 & < y < & 83.0 \end{eqnarray*}$

This is the 95 $\%$ confidence interval for predicting the mark of a person who was absent for 10 days.

▢

Important: $s_{\mbox{set}}$ is independent of $x$ but $E$ is not. So confidence intervals look like :

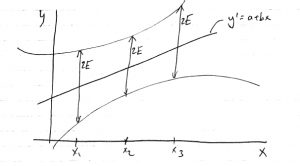
The reason for this variance of the width of the confidence interval comes from the uncertainty in the slope $b$ . You can make plots like the one above in SPSS.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Share This Book