16.2 Median Sign Test

Gordon E. Sarty

16. Non-parametric Tests

16.2 Median Sign Test

The median sign test is a test of a null hypothesis about the median, MD, of a population based on the binomial distribution. To use the test, every subject is assigned a score of $+$ , $0$ or $-$ depending on whether their data point value is greater than, the same as or less than the $H_{0}$ median.

Since the test is based on the binomial distribution, there are two cases we need to consider. One for small samples and one for large samples where the $z$ approximation to the binomial distribution can be used.

Case 1 : small samples ( $n < 26$ ). Here the test statistic is

$X_{\mbox{test}} = \min [(\mbox{no. of $+$}), (\mbox{no. of $-$})]$

and the critical statistic, $X_{\mbox{crit}}$ comes from the Sign Test Critical Values Table for a given $\alpha$ , 1 or 2 tailed test and a value for $n_{s}$ where

$n_{s} = (\mbox{no. of $+$}) + (\mbox{no. of $-$})$

Reject $H_{0}$ if $X_{\mbox{test}} \leq X_{\mbox{crit}}$ .

Case 2 : large samples ( $n \geq 26$ ). With $X_{\mbox{test}}$ as defined for case 1, the test statistic is

$z_{\mbox{test}} = \frac{(X_{\mbox{test}} + 0.5) - (n/2)}{(\sqrt{n}/2)}$

where

$n = (\mbox{no. of $+$}) + (\mbox{no. of $0$}) + (\mbox{no. of $-$}) \neq n_{s}$

the critical statistic is $z_{\mbox{crit}}$ obtained in the usually way using either the Standard Normal Distribution Table or (recommended) the t Distribution Table. Reject $H_{0}$ if $z_{\mbox{test}}$ is in the critical region.

There are 3 sets of hypotheses about the null hypothesis median, $M_{0}$ :

Two-tailed

Left-tailed

Right-tailed

$H_{0}: \mbox{MD} = M_{0}$

$H_{0}: \mbox{MD} \geq M_{0}$

$H_{0}: \mbox{MD} \leq M_{0}$

$H_{1}: \mbox{MD} \neq M_{0}$

$H_{1}: \mbox{MD} < M_{0}$

$H_{1}: \mbox{MD} > M_{0}$

Example 16.3 (Small sample size, case 1.).

Given the following snow cone sales data :

18 43 40 16 22
30 29 32 37 36
39 34 39 45 28
36 40 34 39 52

test the conjecture that the median snow cone sales is 40.

Solution.

0. Data reduction.

Reduce the data to $+$ , $0$ and $-$ signs relative to $M_{0} = 40$ :

$-$ $+$ $0$ $-$ $-$
$-$ $-$ $-$ $-$ $-$
$-$ $-$ $-$ $+$ $-$
$-$ $0$ $-$ $-$ $+$

so (no. of $+$ ) = 3, (no. of $-$ ) = 15 and $n_{s} = 3 + 15 = 18$ .

1. Hypothesis.

$\begin{eqnarray*} H_{0} &:& \mbox{MD} = 40 \\ H_{1} &:& \mbox{MD} \neq 40 \\ \end{eqnarray*}$

2. Critical statistic.

Using the Sign Test Critical Values Table with $n_{s} = 18$ and $\alpha = 0.05$ for a two-tailed test find

$X_{\mbox{crit}} = 4$

3. Test statistic.

$\begin{eqnarray*} X_{\mbox{test}} & = & \min [(\mbox{no. of $+$}), (\mbox{no. of $-$})] \\ & = & \min [3,15] = 3 \end{eqnarray*}$

4. Decision.

$(X_{\mbox{test}} = 3) < (X_{\mbox{crit}} = 4)$

so reject $H_{0}$ .

5. Interpretation.

There is enough evidence to reject the claim that the median number of snow cone sales is 40.

▢

Example 16.4 : (Large sample size, case 2.)

We wish to test the claim that the median lifetime of manufactured rubber washers is greater than or equal to 8 years. We are given the following data from a sample of 50 washers :

21 washers in our sample last more than 8 years
29 washers in our sample last less than 8 years
(none last exactly 8 years).

Solution.

0. Data reduction.

Label the washer that last longer than 8 years with a $+$ and the others with a $-$ . So (no. of $+$ ) = 21 and (no. of $-$ ) = 29.

1. Hypothesis

$H_{0}$ : MD $\geq$ 8 (claim)
$H_{1}$ : MD $<$ 8

2. Critical statistic.

Using the t Distribution Table, last $(z)$ line, $\alpha = 0.05$ for a one-tailed test we find

$z_{\mbox{crit}} = -1.645$

3. Test statistic.

$\begin{eqnarray*} X_{\mbox{test}} & = & \min [(\mbox{no. of $+$}), (\mbox{no. of $-$})] \\ & = & \min [21,29] = 21 \end{eqnarray*}$

so

$\begin{eqnarray*} z_{\mbox{test}} & = & \frac{(X_{\mbox{test}} + 0.5) - (n/2)}{(\sqrt{n}/2)}\\ & = & \frac{(21 + 0.5) - (50/2)}{(\sqrt{50}/2)}\\ & = & \frac{21.5 - 25}{3.5355}\\ & = & -0.99 \end{eqnarray*}$

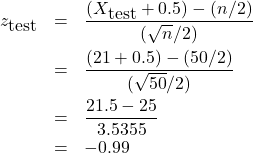
4. Decision.

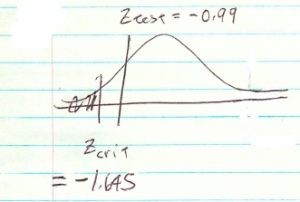
Do not reject $H_{0}$ .

5. Interpretation.

There is not enough evidence, at $\alpha = 0.05$ , to say that washers last less that 8 years.

▢

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Share This Book