"

16. Non-parametric Tests

16.6 Kruskal-Wallis Test (H Test)

The Kruskal-Wallis Test is a non-parametric one-way ANOVA. It detects differences in means between groups. The distribution behind the test is a new discrete distribution called the H distribution that assumes the group samples come from populations with identically shaped distributions. We will use a \chi^{2} approximation of H for computing the critical statistic so, for that approximation, we need n_{i} > 5 for i = 1, 2, \ldots, k, where k is the number of groups. The hypothesis tested is :

H_{0}: means of groups all equal

H_{1}: means of groups not all equal

As mentioned, the critical statistic is \chi^{2}_{\mbox{crit}} with \nu = k - 1 degrees of freedom which we can find using the Chi Squared Distribution Table.

The test statistic is :

    \[ H = \frac{12}{N(N+1)} \left[ \sum_{i=1}^{k} \frac{R_{i}^{2}}{n_{i}} \right] - 3(N+1) \]

where

    \begin{eqnarray*} R_{i} & = & \sum \mbox{ of ranks of group }i \\ n_{i} & = & \mbox{ size of sample }i \\ N &=& \sum_{i=1}^{k} n_{i} \\ k &=& \mbox{ number of groups} \end{eqnarray*}

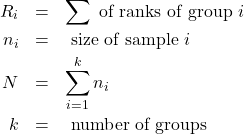
The test is always right-tailed.

 

Example 16.8 : With the following data on ml of potassium/quart in brands of drink, determine if there is a significant difference in the potassium content between brands.

Brand A Brand B Brand C
4.7 5.3 6.3
3.2 6.4 8.2
5.1 7.3 6.2
5.2 6.8 7.1
5.0 7.2 6.6

0. Data reduction.

We need to rank the data. Ranking “in place” we have :

Brand (IV) DV Rank
A 4.7 2
A 3.2 1
A 5.1 4
A 5.2 5
A 5.0 3
B 5.3 6
B 6.4 9
B 7.3 14
B 6.8 11
B 7.2 13
C 6.3 8
C 8.2 15
C 6.2 7
C 7.1 12
C 6.6 10

Using A = 1, B = 2, c = 3, the sums of the ranks for each group are

    \begin{eqnarray*} R_{1} & = & 2 + 1 + 4 + 5 + 3 = 15\\ R_{2} & = & 6 + 9 + 14 + 11 + 13 = 53 \\ R_{3} & = & 8 + 15 + 7 + 12 + 10 = 52 \end{eqnarray*}

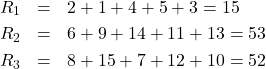
Finally note that n_{1} = n_{2} = n_{3} = 5 and N = 15.

1. Hypothesis.

H_{0} : no differences in means between the brands
H_{1} : some differences exist

2. Critical statistic.

From the Chi Squared Distribution Table with \alpha = 0.05, \nu = k-1 = 3 - 1 = 2 find

    \[ \chi^{2}_{\mbox{crit}} = 5.991 \]

3. Test statistic.

    \begin{eqnarray*} H & = & \frac{12}{N(N+1)} \left[ \sum_{i=1}^{k} \frac{R_{i}^{2}}{n_{i}} \right] - 3(N+1) \\ & = & \frac{12}{15(16)} \left[ \frac{15^{2}}{5} + \frac{53^{2}}{5} + \frac{52^{2}}{5} \right] - 3(16) \\ & = & 9.38 \end{eqnarray*}

4. Decision.

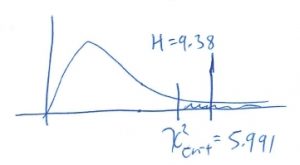
Reject H_{0}.

5. Interpretation.

At least one of the brands is different. Since R_{1} is far less than the rank sums of the other two brands, we know that Brand A is different before we do any kind of post hoc testing.

▢

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book