6. Percentiles and Quartiles
6.1 Discrete Data Percentiles and Quartiles
Before we get into how to calculate percentile in a data set, note that we can see percentiles directly on a cumulative frequency plot, see Figure 6.2.
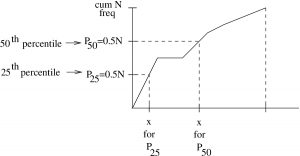
 axis. If you have a newborn baby and take it to the doctor for their first check up, they will measure the baby’s head circumference and tell you the baby’s head size percentile by looking at such a chart. The doctor’s chart will be based on an accumulation of a very large number of essentially population data. Cumulative frequency graphs, or more exactly cumulative probability graphs, can be made for continuous distributions like the normal distribution. The resulting function is the Cumulative Distribution Function, or CDF, and is, for example, P(z) represents the z-distribution then CDF
axis. If you have a newborn baby and take it to the doctor for their first check up, they will measure the baby’s head circumference and tell you the baby’s head size percentile by looking at such a chart. The doctor’s chart will be based on an accumulation of a very large number of essentially population data. Cumulative frequency graphs, or more exactly cumulative probability graphs, can be made for continuous distributions like the normal distribution. The resulting function is the Cumulative Distribution Function, or CDF, and is, for example, P(z) represents the z-distribution then CDF 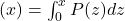 . We will see this CDF in SPSS.
. We will see this CDF in SPSS.Computing percentile positions of discrete data. Let ![]() be the ordered position of a data set of
be the ordered position of a data set of ![]() data points, then we define the percentile position of
data points, then we define the percentile position of ![]() to be
to be
(6.1) ![]()
This formula has the property that ![]() and
and ![]() . It is what we will use as a percentile formula but it is not the only one. Look at Figure 6.1. The way the histogram there is shaded the formula would be
. It is what we will use as a percentile formula but it is not the only one. Look at Figure 6.1. The way the histogram there is shaded the formula would be ![]() which would have the property that
which would have the property that ![]() and
and ![]() . There are other, not necessarily wrong, ways to define the percentile position of discrete data but we will use Equation 6.1.
. There are other, not necessarily wrong, ways to define the percentile position of discrete data but we will use Equation 6.1.
If you want to find the position, ![]() , of the data point corresponding to a given percentile
, of the data point corresponding to a given percentile ![]() then compute
then compute
(6.2) ![]()
Equation (6.2) is derived by solving Equation (6.1) for ![]() . Note that Equation (6.2) gives the position of the data point
. Note that Equation (6.2) gives the position of the data point ![]() , not its value. To clarify that, let’s look at an example.
, not its value. To clarify that, let’s look at an example.
Example 6.1 : Consider the dataset given below. Data would originally be given as the numbers in the first line. So the first step in answering any question about percentiles is to order the data, the same as what you need to to to determine the median of a dataset. Once the data are ordered, then you may assign a position number to each data point as shown in the third line.
| original data | 18 | 15 | 12 | 6 | 8 | 2 | 3 | 5 | 20 | 10 |
| ordered data | 2 | 3 | 5 | 6 | 8 | 10 | 12 | 15 | 18 | 20 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Q : What is the percentile rank of ![]() ?
?
A : ![]() so
so ![]() percentile.
percentile.
Q : What is the value corresponding to the ![]() percentile,
percentile, ![]() ?
?
A : ![]()
The closest ![]() is 3 and
is 3 and ![]() . We can write
. We can write ![]() .
.
▢
Decile :
![]() The decile of data value
The decile of data value ![]() in the ordered position
in the ordered position ![]() is defined as
is defined as
![]()
We will not make much use of decile except to see that quartile is defined in the same way.
Quartile :
![]() The quartile of data value
The quartile of data value ![]() in the ordered position 1.
in the ordered position 1.
(6.3) ![]()
Notation : (This notation also applies to ![]() and
and ![]() .) We write :
.) We write :
![]() &=&
&=& ![]() quartile
quartile
![]() & = &
& = & ![]() quartile
quartile
![]() & = &
& = & ![]() quartile
quartile
![]() & = &
& = & ![]() quartile
quartile
![]() & = &
& = & ![]() quartile
quartile
Quartiles are useful because we do not have to compute percentile first and then divide by 25 as given by Equation (6.3). Instead, we can use the following handy tricks after ordering our data:

Example 6.2 : Example with an even number of data points. With the data in order, first find the median, then the medians of the two halves of the dataset :
![]()
![]()
![]()
![]()
![]()
![]()
▢
Example 6.3 : Example with an even number of data points. With the data in order, first find the median, then the medians of the two halves of the dataset :
![]()
![]()
![]()
![]()
![]()
![]()
▢

