8. Confidence Intervals
8.3 The t-Distributions
As a broad introduction, the ![]() -distributions are family of distributions that give different approximations to the
-distributions are family of distributions that give different approximations to the ![]() -distribution as shown in Figure 8.5.
-distribution as shown in Figure 8.5.
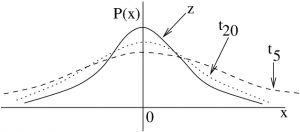
 -distributions are a family of distributions, labeled here by their degrees of freedom
-distributions are a family of distributions, labeled here by their degrees of freedom  as in
as in  .
.As the degrees of freedom, ![]() , increases,
, increases, ![]() become closer to
become closer to ![]() ,
, ![]() . In practice, as reflected in the t Distribution Table,
. In practice, as reflected in the t Distribution Table, ![]() is very very close to
is very very close to ![]() .
.
The ![]() -distributions arise as a corollary to the central limit theorem; they give the distribution of sample means when knowledge of the population
-distributions arise as a corollary to the central limit theorem; they give the distribution of sample means when knowledge of the population ![]() is replaced by using the sample mean
is replaced by using the sample mean ![]() . When we encounter the
. When we encounter the ![]() distribution later, we will give a more exact mathematical specification of the
distribution later, we will give a more exact mathematical specification of the ![]() -distributions.
-distributions.
Similar, to the ![]() -distribution case, the
-distribution case, the ![]() confidence interval for the mean
confidence interval for the mean ![]() for small
for small ![]() samples is given by
samples is given by
![]()
where, now
![]()
With this new formula for ![]() we have replaced
we have replaced ![]() with
with ![]() in comparison with the formula we used in Section 8.1: Confidence Intervals using the z-distribution and, of course, replaced
in comparison with the formula we used in Section 8.1: Confidence Intervals using the z-distribution and, of course, replaced ![]() with
with ![]() . Some books use
. Some books use ![]() like the
like the ![]() of Section 8.1. We use
of Section 8.1. We use ![]() because we’ll look up its value in the t Distribution Table in the column for
because we’ll look up its value in the t Distribution Table in the column for ![]() confidence intervals (just like we did with
confidence intervals (just like we did with ![]() ) and with the degrees of freedom
) and with the degrees of freedom ![]() specifying the row. The formula for the degrees of freedom in this case is :
specifying the row. The formula for the degrees of freedom in this case is :
![]()
The ![]() specify a probability
specify a probability ![]() as shown in Figure 8.6. As before, the inverse
as shown in Figure 8.6. As before, the inverse ![]() -transform, in the form
-transform, in the form ![]() from the
from the ![]() -distribution on the left of Figure 8.6 to the distribution on the right of Figure 8.6 leads to our confidence interval formula for small means. And as before we should justify using that transform from a Bayesian perspective.
-distribution on the left of Figure 8.6 to the distribution on the right of Figure 8.6 leads to our confidence interval formula for small means. And as before we should justify using that transform from a Bayesian perspective.
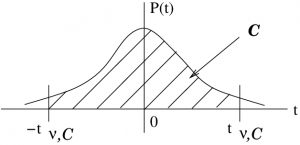 → inverse
→ inverse ![]() -transform →
-transform → 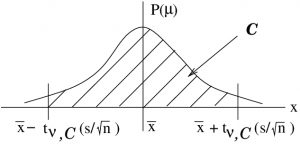
Figure 8.6 : Derivation of confidence intervals for means of small samples.
Example 8.2 : Given the following data:
![]()
find the 99% confidence interval for the mean.
Solution : First count ![]() and then, with your stats calculator compute
and then, with your stats calculator compute
![]()
Using the t Distribution Table with ![]() in the 99% confidence interval column, find
in the 99% confidence interval column, find
![]()
With these numbers, compute
![]()
so
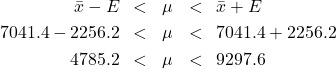
is the 99![]() confidence interval for
confidence interval for ![]() .
.
▢

