9.4 z-Test for Proportions

Gordon E. Sarty

9. Hypothesis Testing

9.4 z-Test for Proportions

The possible hypothesis pairs are :

Two-tailed Test

Right-tailed Test

Left-tailed Test

$H_{0}:p=k$

$H_{0}:p\leq k$

$H_{0}:p\geq k$

$H_{1}:p\neq k$

$H_{1}:p>k$

$H_{1}:p<k$

The steps in hypothesis testing for proportions are the same as hypothesis testing for means. Even the generic test statistic formula is the similar :

$\mbox{test value }=\frac{\mbox{(observed value)-(expected $H_0$ value)}}{\mbox{standard error}}.$

but now the observed and expected values are proportions, $\hat{p}$ and $p$ respectively. The standard error in this case is

$\sqrt{\frac{pq}{n}} = \frac{\sigma_{binomial}}{n} = \frac{\sqrt{npq}}{n}$

Using this information with the generic form, which mimics a $t$ test statistic, the proportions test statistic is

$z_{test} = \frac{\hat{p}-p}{ \sqrt{\frac{pq}{n}}}$

where $p$ is the number $k$ which appears in the $H_{0}$ hypothesis statement (see table above). This test statistic is valid only if $np \geq 5$ and $nq \geq 5$ (so that the normal distribution provides a good approximation for the relevant binomial distribution). But, even though the test statistic can be moulded into the generic form, the proportions test statistic comes from the sampling theory given by the binomial distributions and not from any distribution that has a standard error {\em per se}. The normal distribution with $\mu = np$ and $\sigma = \sqrt{npq}$ (remember those binomial distribution formulae?) $z$ -transformed to a $z$ -distribution with mean 0 and standard deviation 1 gives the test statistic formula. See the discussion in Section 8.4.

Example 9.5 : An attorney claims that more than 25 $\%$ of all lawyers advertise. A sample of 200 lawyers in a certain city showed that 63 had used some form of advertising. At $\alpha = 0.05$ , is there enough evidence to support the attorney’s claim?

Solution :

1. Hypotheses.

$H_{0}: p \leq 0.25$ , $H_{1}: p > 0.25$ (claim)

2. Critical statistic.

Using the t Distribution Table (last line) for a one tailed test at $\alpha = 0.05$ we find $z_{\rm critical} = 1.645$

3. Test statistic.

$z_{\rm test} = \frac{\hat{p} - p}{\sqrt{\frac{pq}{n}}}$

So using

$\hat{p} = \frac{63}{200} = 0.315 \hspace{.25in} p = 0.25$

$q = 1 - 0.25 = 0.75 \hspace{.25in} n = 200$

find

$z_{\rm test} = \frac{0.35 - 0.25}{\sqrt{\frac{(0.25)(0.75)}{200}}} = 2.12.$

We can also find the $p$ value along with the critical statistic. (See the picture for the next step.) Use the Standard Normal Distribution Table to find

$\begin{eqnarray*} p(z) & = & 0.5 - A(z) \\ & = & 0.5 - 0.4830 = 0.017 \\ p & = & 0.017 \end{eqnarray*}$

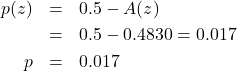
4. Decision.

Refer to the diagram in Figure 9.4. It shows $t_{\rm test}$ in the rejection region. So we reject $H_{0}$ .

Figure 9.4 : The null hypothesis situation for Example 9.5

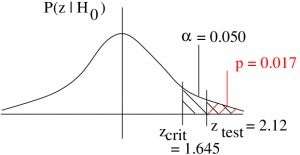
We come, of course, to the same decision by considering the $p$ -value :

$(p = 0.017) < (\alpha = 0.5)$

5. Interpretation.

There is enough evidence, using a $z$ -test at $\alpha = 0.05$ , to support the claim that more than $25\%$ of the lawyers use some form of advertising.

▢

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Share This Book